Much of what I have pinned comes from a source that had the following info. regarding copyright, so wanted to share this: This work © 2006-11 Anneke
Tessellations – Mathigon
Pure Tessellation. A tessellation of only one shape. Regular Tessellation. A tessellation of only one regular polygon. Tessellation. Using repeated shapes to completely cover a plane with no overlaps or gaps. Vertex. The corner of an angle or polygon where two segments or rays meet. Which of the following regular polygons will not tessellate by
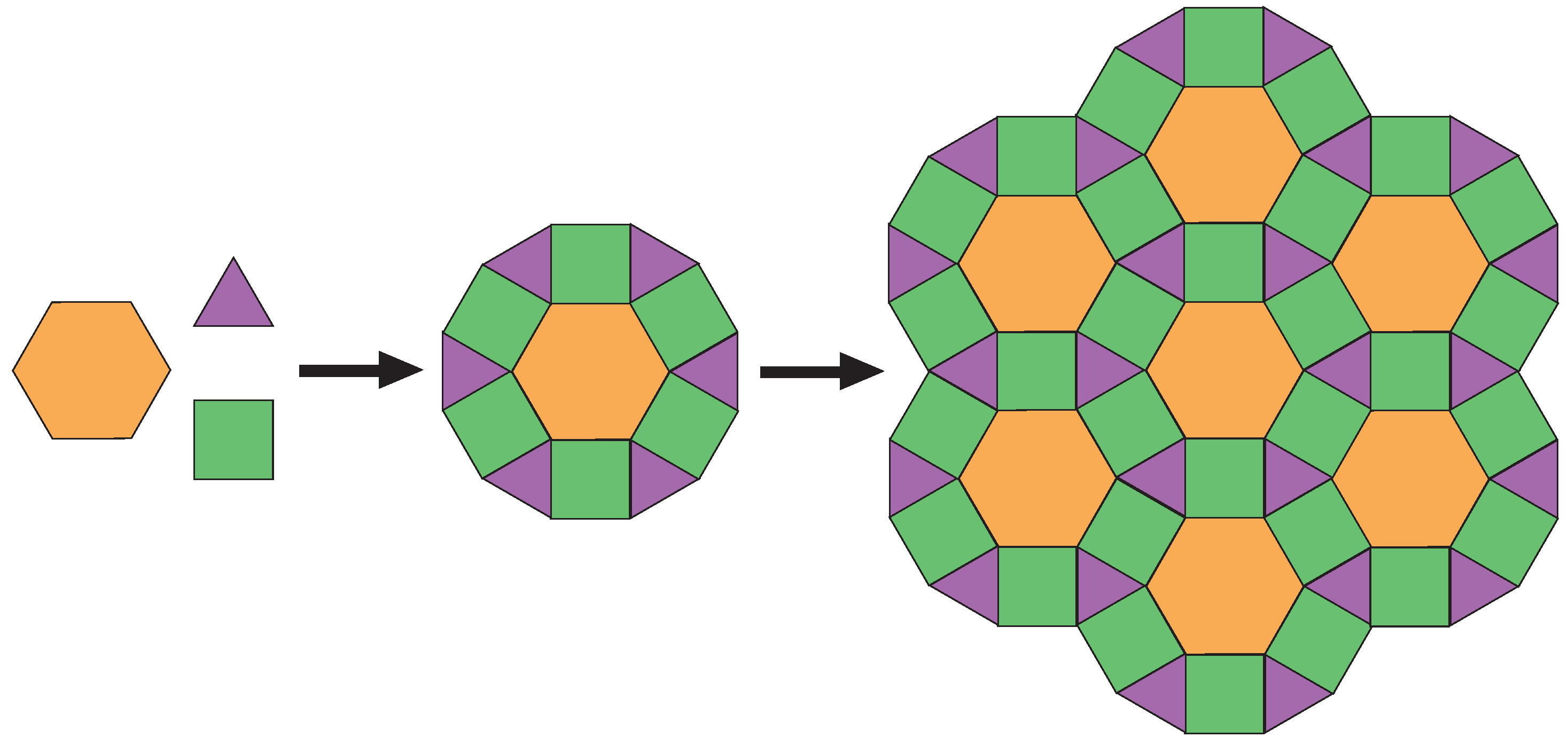
Source Image: mdpi.com
Download Image
Mar 24, 2023Regular Tessellations. A regular shape in mathematics means a shape with equal sides and equal angles. Squares, hexagons, and equilateral triangles are regular shapes that create regular tessellations. Semi-Regular Tessellations. A semi-regular tessellation (also called Archimedean) consists of two or more regular polygons of the same length.

Source Image: mathigon.org
Download Image
Solved Calculate interior angle of regular polygon to check | Chegg.com Regular tessellations. In mathematical terms, “regular” describes any shape that has all equal sides and equal angles. There are three regular shapes that make up regular tessellations: the
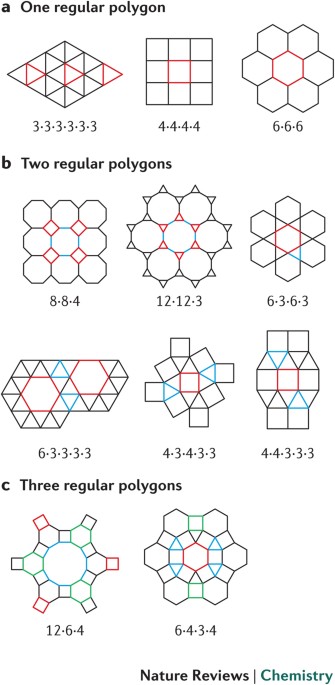
Source Image: nature.com
Download Image
Which Of The Following Best Describes A Regular Tessellation
Regular tessellations. In mathematical terms, “regular” describes any shape that has all equal sides and equal angles. There are three regular shapes that make up regular tessellations: the A tessellation is a pattern of shapes repeated to fill a plane. The shapes do not overlap and there are no gaps. The figure above composed of squares is a tessellation since the are no gaps or overlaps between any 2 squares. The figure above composed of regular pentagons is not a tessellation since there are gaps between the tessellations in grey.
Tessellated multiporous two-dimensional covalent organic frameworks | Nature Reviews Chemistry
For a tessellation of regular congruent polygons, the sum of the measures of the interior angles that meet at a vertex equals. 360 ∘. 360 ∘. In Figure 10.78, the tessellation is made up of squares. There are four squares meeting at a vertex. An interior angle of a square is 90 ∘ and the sum of four interior angles is 360 ∘. Semi-Regular Tessellation | Definition, Types & Examples | Study.com

Source Image: study.com
Download Image
Tessellation Shapes, Patterns & Examples – Video & Lesson Transcript | Study.com For a tessellation of regular congruent polygons, the sum of the measures of the interior angles that meet at a vertex equals. 360 ∘. 360 ∘. In Figure 10.78, the tessellation is made up of squares. There are four squares meeting at a vertex. An interior angle of a square is 90 ∘ and the sum of four interior angles is 360 ∘.

Source Image: study.com
Download Image
Tessellations – Mathigon Much of what I have pinned comes from a source that had the following info. regarding copyright, so wanted to share this: This work © 2006-11 Anneke
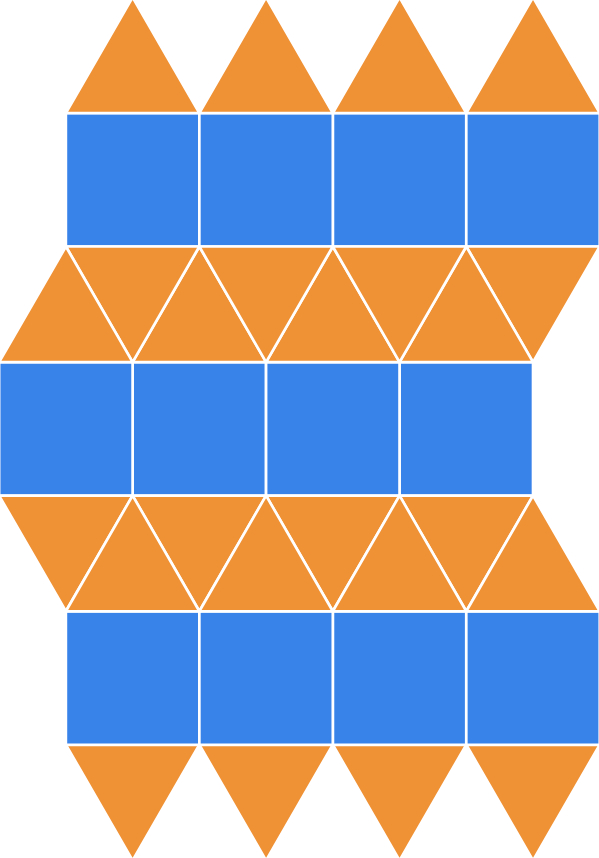
Source Image: mathigon.org
Download Image
Solved Calculate interior angle of regular polygon to check | Chegg.com Mar 24, 2023Regular Tessellations. A regular shape in mathematics means a shape with equal sides and equal angles. Squares, hexagons, and equilateral triangles are regular shapes that create regular tessellations. Semi-Regular Tessellations. A semi-regular tessellation (also called Archimedean) consists of two or more regular polygons of the same length.
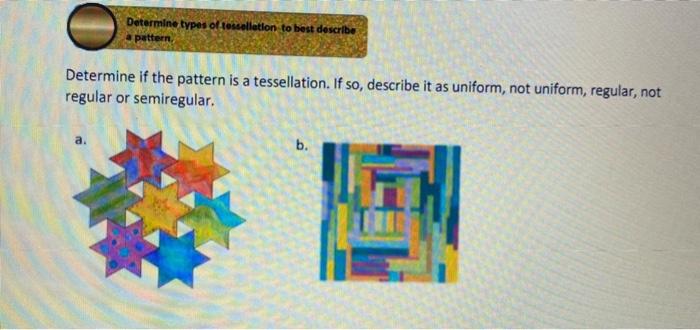
Source Image: chegg.com
Download Image
Semester Project a tessellation of only one regular polygon. tessellation. using repeated shapes to completely cover a plane with no overlaps or gaps. vertex. the corner of an angle or polygon where two segments or rays meet. Pure tessellations can only be made with regular polygons. False. In order for polygons to tessellate, the total number of degrees where

Source Image: 5010.mathed.usu.edu
Download Image
Tessellations (4): Semi-Regular Tessellations | Tessellation patterns, Study unit, Math Regular tessellations. In mathematical terms, “regular” describes any shape that has all equal sides and equal angles. There are three regular shapes that make up regular tessellations: the
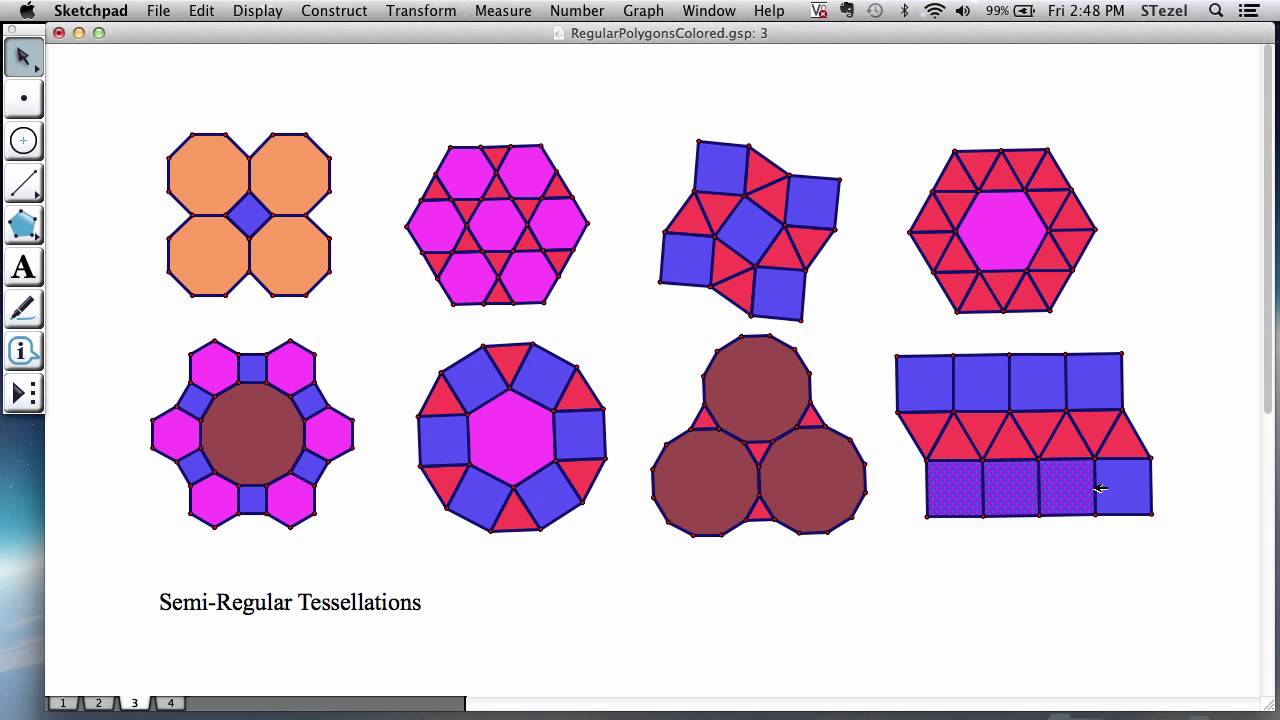
Source Image: pinterest.com
Download Image
A Tessellation of Regular Polygons for the New Year MMXIV | RobertLovesPi.net A tessellation is a pattern of shapes repeated to fill a plane. The shapes do not overlap and there are no gaps. The figure above composed of squares is a tessellation since the are no gaps or overlaps between any 2 squares. The figure above composed of regular pentagons is not a tessellation since there are gaps between the tessellations in grey.

Source Image: robertlovespi.net
Download Image
Tessellation Shapes, Patterns & Examples – Video & Lesson Transcript | Study.com
A Tessellation of Regular Polygons for the New Year MMXIV | RobertLovesPi.net Pure Tessellation. A tessellation of only one shape. Regular Tessellation. A tessellation of only one regular polygon. Tessellation. Using repeated shapes to completely cover a plane with no overlaps or gaps. Vertex. The corner of an angle or polygon where two segments or rays meet. Which of the following regular polygons will not tessellate by
Solved Calculate interior angle of regular polygon to check | Chegg.com Tessellations (4): Semi-Regular Tessellations | Tessellation patterns, Study unit, Math a tessellation of only one regular polygon. tessellation. using repeated shapes to completely cover a plane with no overlaps or gaps. vertex. the corner of an angle or polygon where two segments or rays meet. Pure tessellations can only be made with regular polygons. False. In order for polygons to tessellate, the total number of degrees where